Pattern Matching

Pattern Matching

Given a pattern \(P\) and a text \(T\) find the first/all occurances of the pattern \(P\) inside of text \(T\).

Find the index of the first occurrence in a string (leetcode question 28).

Note: Every algorithm listed here only makes sense if you are not allowed to compute an index on the text. Therefore, this is not suitable for things like search engines.

All these algorithm require at least \(O(m + n)\) running time, if the text gets large enough, then we won’t be able to find the pattern in reasonable time. These algorithms are suitable when the text is dynamic in nature – like a text editor or on a singular web page (Ctrl-F on your browser).

For searching with precompute, refer to the following notes page: https://old.suchicodes.com/resources/blog/14222f2d#text-indexing-structures

Brute-force Method

Just compare substring with every possible position in the original string.

def strStr(haystack: str, needle: str) -> int:
    for i in range(len(haystack)):
        if haystack[i:i+len(needle)] == needle:
            return i
    return -1

This requires \(O(nm)\) running time as at each iteration, we have to iterate over the entire substring.

Knuth-Moris-Pratt (KMP) Algorithm

The Knuth-Moris-Pratt is an algorithm that preprocesses the pattern to build a longest prefix-suffix table (LPS table), then scan the text efficiently using that table.

Here is a good video explaining the algorithm: https://youtu.be/ynv7bbcSLKE.

The longest prefix suffix of a pattern is the longest prefix that matches a proper suffix of the substring ending at a given position. The KMP algorithm first builds a table of the longest prefix suffix at every index.

Example: «abab» has a longest prefix «ab» because it is both a prefix and a suffix but not the whole string itself.

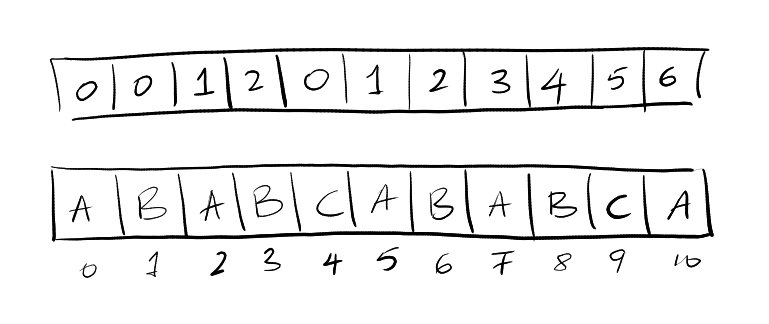
Here are few examples explained visually:

We can compute this table using the following code:

def LPS(pattern):
    m = len(pattern)
    lps = [0] * m
    j = 0
    i = 1

    while i < m:
        if pattern[i] == pattern[j]:
            j += 1
            lps[i] = j
            i += 1
        else:
            if j != 0:
                j = lps[j - 1]
            else:
                lps[i] = 0
                i += 1

    return lps

• lps[0] is always 0 since a single character has no proper prefix or suffix.
• i traverses the pattern from left to right.
• j tracks the length of the current matching prefix-suffix.

If the characters at positions i and j match, increment j as we are existing the current prefix-suffix match by 1 and assign it to lps[i].

def strStr(self, haystack: str, needle: str) -> int:
    i = 0
    j = 0
    m = len(needle)
    n = len(haystack)
    lps = LPS(needle)

    while i < n:
        if needle[j] == haystack[i]:
            i += 1
            j += 1
            if j == m:
                return i - m
        else:
            if j != 0:
                j = lps[j-1]
            else:
                i += 1

    return -1

Boyer-Moore Algorithm

Boyer-Moore uses bad character and good suffix heuristics to skip sections of the text. It runs in \(O(n + m)\) but can degrade to \(O(nm)\) without good heuristics. However, in the best case it runs in sublinear time and average performance is excellent – we end up skipping processing a lot of the characters!

Ben Langmead has a great video explaining Boyer-Moore: https://www.youtube.com/watch?v=4Xyhb72LCX4.

In Boyer-Moore, we compare the text and the pattern right to left. We do this so that when there is a mismatch, we can skip ahead a lot more characters. The algorithm is based off two rules:

Bad Character Rule

When scanning from right to left, if we find a mismatch in the character, we have one of two case: If the character doesn’t exist in the pattern, we can skip so that the whole pattern is now after the character. If the character does exist, we can move the pattern until the mismatch becomes a match.

Good Suffix Rule

If \(t\) is the substring that’s matched so far in the pattern, then we skip until there are no mismatches between \(P\) and \(t\) or \(P\) moves past \(t\). This can happen by either matching the suffix matches with an internal substring or a prefix of \(P\) that matches the suffix of \(t\).

Overall Algorithm

We align the pattern starting from the left going to the right and at each alignment, we compare starting from the right going to the left. Everytime we have a mismatch, we just check both rules and we skip whichever gives us the higher number.

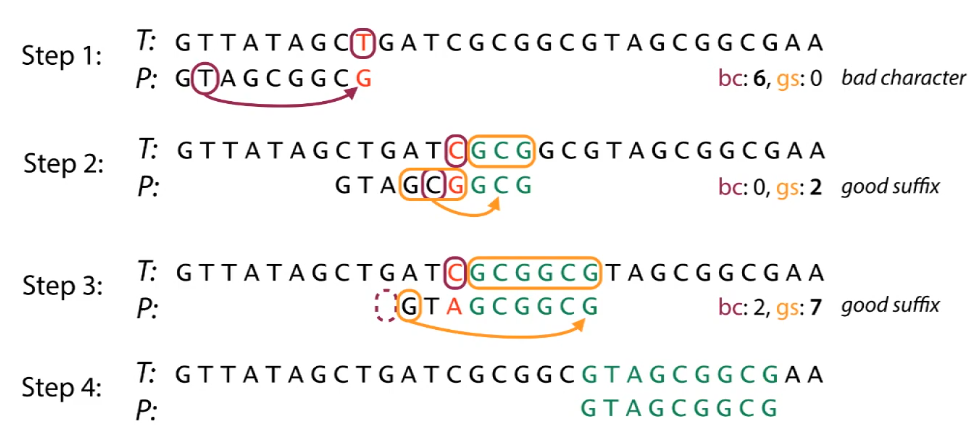
Rabin-Karp Algorithm

Rabin-Karp just uses a rolling hash function to first hash the pattern and then iterate over the text, comparing hashes.

Here’s a good video about it: https://youtu.be/yFHV7weZ_as?.

def rabin_karp(text: str, pattern: str) -> int:
    base = 256
    prime = 1000000007
    n = len(text)
    m = len(pattern)
    bpm = b ** (m-1)

    hash_pat = 0
    hash_txt = 0

    # compute initial hash values at the start
    for i in range(m):
        hash_pat = (base * hash_pat + ord(pattern[i])) % prime
        hash_txt = (base * hash_txt + ord(text[i])) % prime

    # slide pattern over text one-by-one
    for i in range(n - m + 1):
        if hash_pat == hash_txt:
            # if hash match, check if pattern match
            if text[i:i+m] == pattern:
                return i

        # roll hash by one character
        hash_txt = (hash_txt - ord(text[i]) * bpm) * base + ord(text[i+m])
        hash_txt = hash_txt % prime
    
    return -1

Which Algorithm Should I Use?

This is a table that was generated by ChatGPT:

Scenario	Characteristics	Recommended Algorithm	Why
Small text, small pattern	n, m ≤ 100	Naive Search	Minimal overhead; fastest in practice
Medium text, medium pattern	n, m ≤ 10⁴	KMP	Safe, linear, low memory, no hash issues
Large text, short pattern	e.g. text with millions of chars, pattern ≤ 100	Boyer-Moore-Horspool (BMH)	Very fast in practice due to large skips
Large text, repetitive pattern	pattern like "aaaaaa"	KMP	Handles repeated characters without slowdowns
Very large text, many searches	same pattern reused	KMP with precomputed LPS	Build once, reuse
Search for multiple patterns	e.g. blacklist scan	Aho-Corasick	Trie + BFS — finds all patterns in one pass
Binary/text with small alphabet	DNA (A,C,G,T), binaries	KMP or Suffix Automaton	BMH performs poorly on low entropy
Text or pattern is hashed	e.g. plagiarism detection	Rabin-Karp	Fast rolling hash, cheap equality checks
Find all occurrences	not just first match	KMP or Rabin-Karp (with hash verify)	Built for this; BMH doesn’t help
Memory-constrained	low RAM, embedded device	Naive or BMH	Low footprint
Worst-case resistance	avoid pathological slowdowns	KMP or Boyer-Moore Full	Guaranteed linear time
Unicode / multibyte input	e.g. UTF-8 or wide strings	KMP, Naive, or locale-aware tools	Hash-based approaches can break on encoding boundaries

More Algorithms To Explore

1. Boyer-Moore-Horspool (BMH): only bad-character rule from Boyer-Moore, runs with less overhead.

2. Aho-Corasick: find all search patterns in text in a single pass using Tries + BFS.