Algorithms

Algorithms

A quick reference sheet for different algorithms and possible python/go/c implementation of said algorithms.

Floyd’s Cycle Finding Algorithm

Floyd’s cycle finding algorithm is used to detect if a cycle exists in a linked list while using \(O(1)\) extra space. It uses two pointers going at different «speeds» – if a cycle exists, at some point the faster pointer circles the slower pointer.

This algorithm is also known as the fast and slow pointer method of finding a cycle in a linked list.

def hasCycle(head: ListNode) -> bool:
    if head is None:
        return False

    slow = head
    fast = head.next

    while slow != fast:
        if fast is None or fast.next is None:
            return False

        slow = slow.next
        fast = fast.next.next

    return True

This algorithm runs in \(O(n)\) time. We make at most \(\frac{\text{distance between the 2 runners}}{\text{difference of speed}}\) loops for the fast runner to catch up with the slow runner. The distance is at most cyclic length \(K - 1\), we run at most cycle length \(K-1\) times.

Boyer-Moore Voting Algorithm

The Boyer-Moore voting algorithm is used to find the majority element in an array. The majority element is an element that occurs more than \(n/2\) number of times.

This algorithm works by making a candidate majority element and keeping track of it’s «majority» in the current prefix array. It’s obvious that if we have the «correct» candidate then the sum at the end is going to be some positive non-zero integer.

However, when the count of the current candidate reaches 0, we can forget about everything until then because in that second of the array, there does not exist a majority element. Therefore, if there were to be a majority element, it must have a majority in the rest of the array.

Example: [ 1, 1, 1, 3, 4, 5 | 4, 4, 1, 1, | 1, 1 ]
at each point where a pipe exists, the count reset to 0, and therefore we can ignore everything before the pipe. There does not exist a majority in that section and therefore, if there exists a majority, it must be in the next part.

def majorityElement(self, nums):
    count = 0
    candidate = None

    for num in nums:
        if count == 0:
            candidate = num
        
        if num == candidate:
            count += 1
        else:
            count -= 1


    # if we are unsure if a majority element exists,
    # we can check in O(n) time
    # sum(num == candidate for num in nums) > n // 2
    return candidate

Longest Common Subsequence

Find the longest common subsequence between two strings \(s_1\) and \(s_2\). For example, LCS between hello world and hey low would be helow.

Recursion

If we consider part of \(s_1\) and \(s_2\) then we notice that the LCS of \(s_1[1..i]\) and \(s_2[1..j]\) is going to follow the rule:

\[ LCS(i, j) = \begin{cases} LCS(i-1, j-1) + 1 & \text{if } s_1[i] == s_2[j] \\ max(LCS(i-1, j), LCS(i, j-1)) & \text{otherwise} \end{cases} \]

In other words, if the last characters match, we use that in the subsequence and then call the function recursively for the rest. If they don’t the must mean that both of the last characters aren’t used – so we can take the max of the two other cases.

If we implement this without caching it’s going to take \(O(2^{min(m,n)})\) time. However, if we memoize the function, then it will take \(O(mn)\) as it won’t re-explore branches.

from functools import cache

@cache
def LCS(s1, s2):
    m, n = len(s1), len(s2)

    if m == 0 or n == 0:
        return 0
    
    if s1[m-1] == s2[n-1]:
        return 1 + LCS(s1[:m-1], s2[:n-1])
        
    else:
        return max(
            LCS(s1[:m-1], s2),
            LCS(s1, s2[:n-1])
        )

NOTE: you can optimize the code to not create so many new strings but this is done above for code clarity.

DP Using Table

First, let the x-axis be string \(s_1\) and the y-axis be \(s_2\), we will include a null character to denote the empty string \(\epsilon\).

We know that the LCS is 0 when either string is empty. Therefore, this fills our first row and first column with zeros. After this, we notice any cell depends on three values – the cell above, to the left, or diagonally top-left. Since we have the first row and the first column, if we just fill the table from left to right, we will guarantee that we always have the value for any given cell.

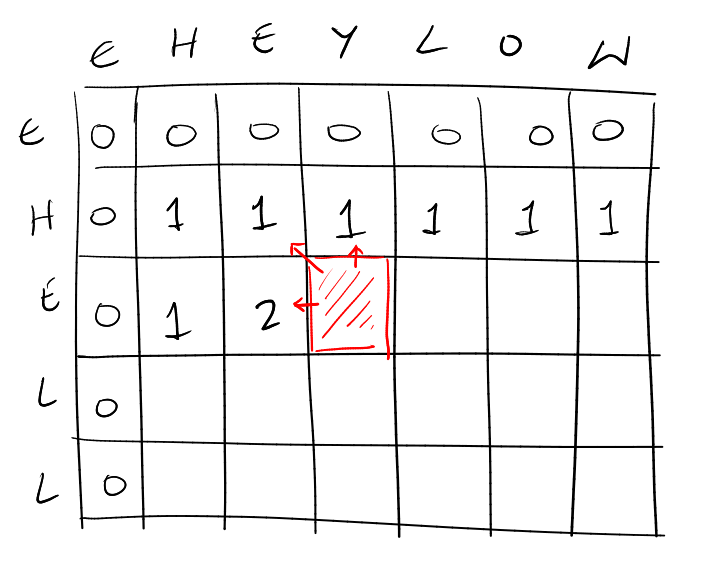
If we wish to not just find the length of the common subsequence but also the actual string, then we can keep track of the choice made at each cell so that we can backtrack to build the string.

top_left = 0
left = 1
top = 2

def lcs(s1, s2):
    m, n = len(s1), len(s2)

    # create a n+1 by m+1 table
    dp = [[(0, None)] * (n+1) for x in range(m+1)]
    
    for i in range(1, m+1):
        for j in range(1, n+1):
            if s1[i-1] == s2[j-1]:
                dp[i][j] = (dp[i-1][j-1][0] + 1, top_left)
            else:
                dp[i][j] = max(
                    (dp[i-1][j][0], top),
                    (dp[i][j-1][0], left),
                    key=lambda x: x[0]
                )

    # build string using back-tracking
    lpc = dp[m][n]
    string = []
    i, j = m, n
    while i != 0 or j != 0:
        _, direction = dp[i][j]
        if direction == top_left:
            string.append(s1[i])
            i, j = i-1, j-1
        elif direction == left:
            i = i - 1
        else:
            j = j - 1
            
    return "".join(reversed(string))

Optimization: Notice that we only need one row above the current rwo while performing the computation. Therefore, it is possible to only keep two rows and compute the LPC. This reduces space from \(O(mn)\) to \(O(min(m,n))\)

The algorithms runs in \(O(mn)\) and needs \(O(mn)\) auxiliary space.

Research Note: There is no faster algorithm than \(O(mn)\) without having to assume a constant alphabet size. \(O(n^2 / lg (n^2))\) is possible with constant alphabet.

Longest Palindromic Subsequence

We can find the longest palindromic subsequence in a string by just reversing the string and finding the longest common subsequence.

def LPS(s):
    return LPC(s, s[::-1])

This can also be done in a more direct way using DP but it doesn’t really save on time.

Research Note: This is the fastest known method for computing the palindromic subsequence asymptotically using worst-case analysis.

Longest Palindromic Substring

Find the longest substring in a given string s that is a palindrome.

If we use a brute-force approach, it would require \(O(n^3)\) time as we would generate all possible substring in \(O(n^2)\) and for each generated string, we would check if it’s a palindrome in \(O(n)\) time.

DP Using Table

If we know that s[i:j] is a palindrome, then we can if s[i-1:j+1] is a palindrome by just checking s[i-1] == s[j+1]. If s[i:j] is not a palindrome, there is no way for s[i-1:j+1] to be a palindrome.

So we build a table of size \(n \times n\) where dp[i][j] is True if s[i:j] (inclusive bounds) is a palindrome. We know that all string of length 1 are palindromes, and we also know that strings of length 2 are palindromes if the two characters match.

def LPSub(s):
    n = len(s)
    dp = [[False] * n for _ in range(n)]
    ans = [0, 0]  # keep track of the longest palindrome range
    
    # single characters are palindromes
    for i in range(n):
        dp[i][i] = True

    # check two character palindromes
    for i in range(n - 1):
        if s[i] == s[i + 1]:
            dp[i][i + 1] = True
            ans = [i, i + 1]
            
    for diff in range(2, n):
        for i in range(n - diff):
            j = i + diff
            if s[i] == s[j] and dp[i+1][j-1]:
                dp[i][j] = True
                ans = [i, j]

    i, j = ans
    return s[i:j+1]

We only use the upper triangle of the dp matrix/table as for a valid substring i <= j. This requires \(O(n^2)\) running time and \(O(n^2)\) auxiliary space.

Expand from Centers

We can just grow palindrome checks from all positions within the string, characters and spaces in-between, to find all possible palindromes.

def expand(i, j):
    left = i
    right = j

    while left >= 0 and right < len(s) and s[left] == s[right]:
        left -= 1
        right += 1
    
    return right - left - 1

def LPSub(s):
    ans = [0, 0]
    ans_len = 1

    for i in range(len(s)):
        odd_len = expand(i, i)
        if odd_len > ans_len:
            dist = odd_len // 2
            ans_len = odd_len
            ans = [i - dist, i + dist]

        even_len = expand(i, i+1)
        if even_len > ans_len: 
            dist = (even_len // 2) - 1
            ans_len = even_len
            ans = [i - dist, i + dist + 1]

    i, j = ans
    return s[i : j + 1]

This still requires \(O(n^2)\) time but it only need \(O(1)\) auxiliary space. This algorithms is also going to have a better average running time as we don’t explore all possible palindromes. Most centers will not produce long palindromes, so most of the calls to expand will cost far less than n iterations.

Manacher’s Algorithms

This algorithms solves the problem of finding the largest palindrome substring in \(O(n)\) time and space! Certainly a great accomplishment!

Thanks to Tushar Roy for helping me understand the algorithm better.

The premise of the algorithm is a rather simple one. We start by choosing a center and finding out the palindrome around that center.

First, we are only going to look at odd-length palindromes and we will show later how to generalize this to even-length palindromes.

To understand the algorithms, let’s assume we’ve calculated the length of the palindromes around the centers so far. That is, at index 3 with center D there is a palindrome of length 7: ACADACA

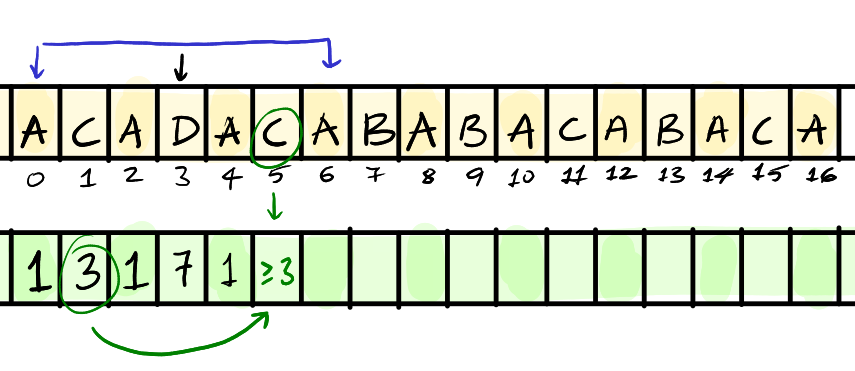
Observations:

1. Since there is a palindrome around D, that mean the characters are mirrored on the other side.

2. This tells us that the A right after must also have a palindrome length of 1 because the A before had a palindrome length of 1. This is because a length of 1 is fully contained within the palindrome.

3. At C, we know that the length of the palindrome is at least 3 as it was 3 on the other side. We do not know if it’s larger because 3 causes the palindrome around C to expand until the edge of the palindrome of D.

Therefore, we already have two optimizations:

1. For every character to the left of the current palindrome, the corresponding character on the right has at least the same palindrome length.

2. If the length of the palindrome on the left, doesn’t reach the left edge (or the right edge of the character on the right) then we know that it’s also the max length. To clarify this – since the palindrome around the A at index 2 does not reach the left edge of our current palindrome, we know that the A at index 4 must also have a palindrome of exact length 1. But in the case of C at index 1, since the palindrome reach the edge of our current palindrome, we can only say that it’s at least length 3 for the C at index 5.

Our new center that we expand upon should be C, the first character who’s length we are not certain of. We can also skip the first character since we know the length is at least 3, we start from B.

NOTE: the next example is slightly different from the previous example to demonstrate a different edge case.

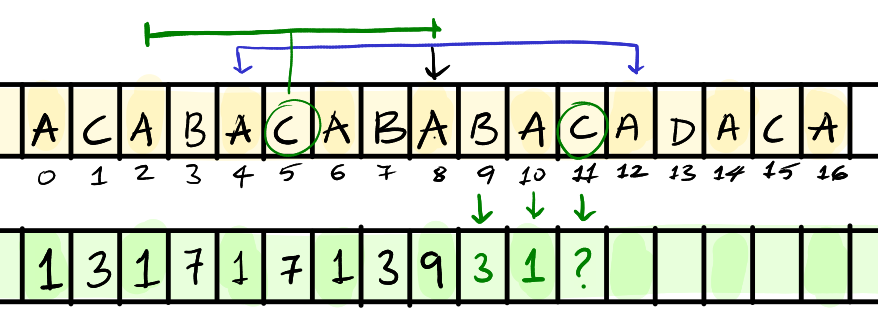
Here, we have a new case to consider. When the palindrome on the left goes past the current palindrome, we can be sure that the palindrome on the right does not expand past the end of our current palindrome. This is because, if it did, then that would mean it would be mirrored on the left as well, which would increase the size of our current palindrome.

1. We know B at 9 doesn’t do past 3 since it’s fully contained in the current palindrome and doesn’t reach the edge.

2. Similar case for A at 10.

Now, even though C goes past the edge on the right side, since the left side palindrome does past our current palindrome, the C on the right cannot have a palindrome long then the edge of our current palindrome. In fact the palindrome at C is going to extend to exactly the edge of our current palindrome.

We know this because, if the palindrome at C at 11 went beyond the edge, it would be mirrored on the left or our current palindrome, extending our current palindrome – which we know is not true. Consider that the D at 13 was actually B, then the palindrome around A at 8 would also expand!

Therefore, the length of the palindrome at C is 3 and A at 12 reaches the edge and the corresponding left palindrome doesn’t go past the edge – therefore it’s going to be our next center to expand around.

Algorithms:

We pick the next possible center to expand around considering:

1. If the new center’s palindrome is totally contained under the current palindrome – we know the length
2. The new center’s mirror palindrome expands beyond the left edge of the current palindrome – we know the length.
3. If the current palindrome expands till end of input – we know the remaining lengths.
4. If the palindrome expands till right edge and the mirror palindrome is a proper prefix of the current palindrome – we start with this as the new center.

Accommodate Even-length Palindromes:

We just process the string s by inserting a placeholder character around each existing character: HELLO –> %H%E%L%L%O%

By doing this, we have now accommodated even-length palindromes as well. We just remove the placeholders after all operations are complete. If we want the length, it’s just the floor of the length divided by 2.

Here’s an example of mapping between both odd and even length palindromes to the new string:

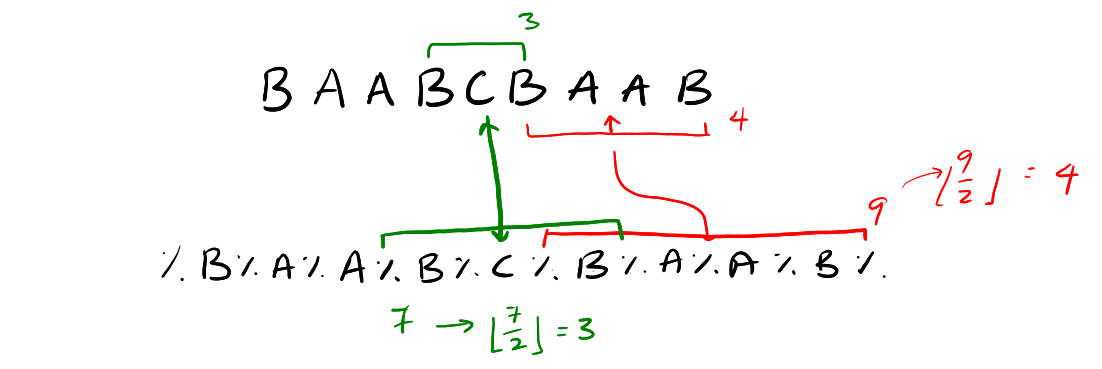
This new string is of length \(2n + 1\) and the Manacher’s algorithm needs \(O(n)\) time so we still have linear time and space used.

Note: It is possible to optimize the algorithm to not have to do redundant processing and use extra space by carefully account for both odd and even length palindromes.

I don’t have the time to optimize for that right now, so here’s a small todo list:

1. Build a look up table for if certain substring is a palindrome.
2. Optimize code to not convert input string using placeholder characters.

Implementation:

def manacher(s):
    # 2025-08-01
    # Tested against test cases on leetcode
    T = "%" + "%".join(s) + "%"
    n = len(T)
    P = [0] * n
    center, right = 0, 0

    max_p = 0
    max_i = 0
    
    for i in range(n):
        mi = 2 * center - i  # mirror index

        if i <= right:
            # We are still inside current palindrome

            if right - i < P[mi]:
                # mirror palindrome goes past left boundary
                P[i] = right - i
                continue

            if right - i > P[mi]:
                # fully contained in palindrome
                P[i] = P[mi]
                continue

            P[i] = P[mi]

        # expand around i
        while (
            i + P[i] + 1 < n and
            i - P[i] - 1 >= 0 and
            T[i + P[i] + 1] == T[i - P[i] - 1]
        ):
            P[i] += 1

        if max_p < P[i]:
            max_p, max_i = P[i], i

        center = i
        right = i + P[i]

    start = (max_i - max_p) // 2  # adjust for '#'
    return s[start:start + max_p]

A few details:

• P holds the radii of the palindromes. A palindrome of size 1 has radius 0.
• center holds the center of the «current» palindrome.
• right holds the right boundary character index of the «current» palindrome.

The running time of this algorithm is \(O(n)\) and it requires \(O(n)\) auxiliary space.

TODO:

1. Write a proof for the running time analysis
2. Optimize the algorithm as detailed above.

Here is the cp-algorithms version of the algorithm. It has a few implicit cases like not checking if the boundaries match of the palindromes as if they don’t, the while loop just fails the check directly. This version of the code may be easier to maintain if you know everything about the algorithm.

• The while loop doesn’t run body for case 1 and 2 – completely within current palindrome or goes past current palindrome.

• The $ and the ^ allows the while loop to ignore checking boundary condition of index of i - p[i] and i + p[i] because p[i] acts as the check itself.

• We have the check i + p[i] > r at the end because we don’t exit early for the cases we can.

vector<int> manacher_odd(string s) {
    int n = s.size();
    s = "$" + s + "^";
    vector<int> p(n + 2);
    int l = 0, r = 1;
    for(int i = 1; i <= n; i++) {
        p[i] = min(r - i, p[l + (r - i)]);
        while(s[i - p[i]] == s[i + p[i]]) {
            p[i]++;
        }
        if(i + p[i] > r) {
            l = i - p[i], r = i + p[i];
        }
    }
    return vector<int>(begin(p) + 1, end(p) - 1);
}

Dijkstra’s Shortest Path Algorithm

Dijkstra’s algorithm is used to find shortest path to all vertices from a given start node. It assumes that all edge weights are non-negative values. This allows Djikstra’s algorithm to be more efficient than Bellman-Ford.

The running time of Dijkstra’s algorithm is \(O((V + E) \lg V)\) where \(V\) is the number of vertices and \(E\) is the number of edges, if we use a binary heap as the priority queue.

If we use a Fibonacci heap to implement the priority queue, the running time can be improved to \(O(V \lg V + E)\).

Implementation

If we want to track the shortest distances to all nodes and then also have the ability to find the shortest path, we can use something like:

def dijkstra(adj_list, start):
    dist = {node: float('inf') for node in adj_list}
    prev = {node: None for node in adj_list}
    dist[start] = 0
    prev[start] = None

    # distance, current node
    pq = [(0, start)]
    
    while pq:
        cur_dist, cur_node = heapq.heappop(pq)

        if cur_dist > dist[cur_node]:
            continue

        for nbor, weight in adj_list[cur_node]:
            dist_nbor = cur_dist + weight
            if dist_nbor < dist[nbor]:
                dist[nbor] = dist_nbor
                prev[nbor] = cur_node
                heapq.heappush(pq, (dist_nbor, nbor))

    return dist, prev

def find_path(start, end, prev_dict):
    cur = end
    path = []

    while cur is not None:
        path.append(cur)
        cur = prev_dict[cur]

    if path[-1] != start:
        return None  # path does not exist

    path.reverse()
    return path

Notes:

1. If you don’t want to build the path later, you can completely ignore the prev hashmap.
2. If you don’t want shortest path to all nodes but rather to a single node, you can replace dist with a visited set instead. Then, we just keep going until we see the destination node – we can stop and return the current cost.

Constrained Dijkstra

If we want to get the shortest path but we want to satisfy some other constraint like number of steps or a different cost, we can modify dijkstra slightly to achieve this.

Example: LeetCode question 1928 is about reaching a destination with minimum cost given a maximum time. Each node has an associated visit cost and each edge has a time to travel. We want to reach the destination within the time limit while minimizing the cost paid.

There is a country of n cities numbered from 0 to n – 1 where all the cities are connected by bi-directional roads. The roads are represented as a 2D integer array edges where edges[i] = [xi, yi, timei] denotes a road between cities xi and yi that takes timei minutes to travel. There may be multiple roads of differing travel times connecting the same two cities, but no road connects a city to itself.

Each time you pass through a city, you must pay a passing fee. This is represented as a 0-indexed integer array passingFees of length n where passingFees[j] is the amount of dollars you must pay when you pass through city j.

In the beginning, you are at city 0 and want to reach city n – 1 in maxTime minutes or less. The cost of your journey is the summation of passing fees for each city that you passed through at some moment of your journey (including the source and destination cities).

Given maxTime, edges, and passingFees, return the minimum cost to complete your journey, or -1 if you cannot complete it within maxTime minutes.

Now we just need to account for the time taken – we don’t just throw out if the cost is higher, we throw out if the cost and time are both highest. We first explore the lost cost path, if we can’t make it within the given time, we explore the higher cost path.

class Solution:
    def buildAdjList(self, edges):
        adj = defaultdict(list)
        for x, y, time in edges:
            adj[x].append((y, time))
            adj[y].append((x, time))
        return adj

    def minCost(self, maxTime: int, edges: List[List[int]], passingFees: List[int]) -> int:
        adj = self.buildAdjList(edges)
        dst = len(passingFees) - 1

        times = {}

        # cost, time, node
        pq = [(passingFees[0], 0, 0)]

        while pq:
            cost, time, node = pop(pq)

            if time > maxTime:
                continue

            if node == dst:
                return cost

            # if path has higher cost and higher time, throw it away
            if node not in times or times[node] > time:
                times[node] = time
                for nbor, weight in adj[node]:
                    push(pq, (passingFees[nbor] + cost, time + weight, nbor))

        return -1

Topological Sort

If we have a directed graph and we treat a inward-edge as a dependency, that is, if edge \((x, y)\) (x->y) exists then we must first visit x before visiting y. The most common example of requiring a topological sort is when we have courses in university that have pre-requisites – you must complete all pre-requisites before taking course y.

A topological ordering is an ordering of the nodes in a directed graph where for each directed edge from node \(A\) to node \(B\), node \(A\) appears before node \(B\) in the ordering. Only directed acyclic graphs (DAG) have topological orderings.

DFS is a common way to implement a topological sort by just running DFS from all vertices without any «dependencies». Another popular algorithm is Kahn’s algorithm.

DFS-Based Topological Sort

class Node:
    def __init__(self, value):
        self.value = value
        self.neighbors = []

class Graph:
    def __init__(self):
        self.nodes = {}

    def add_node(self, value):
        if value not in self.nodes:
            self.nodes[value] = Node(value)

    def add_edge(self, from_node, to_node):
        self.add_node(from_node)
        self.add_node(to_node)
        self.nodes[from_node].neighbors.append(self.nodes[to_node])

    def topological_sort(self):
        visited = set()
        stack = []
        temp_mark = set()  # Detect cycles

        def dfs(node):
            if node in temp_mark:
                raise ValueError("Graph contains a cycle")
            if node in visited:
                return

            temp_mark.add(node)
            for neighbor in node.neighbors:
                dfs(neighbor)

            # cycle if we visit same node within one DFS search but not if
            # visit node in two different DFS searches.
            temp_mark.remove(node)

            visited.add(node)
            stack.append(node.value)

        for node in self.nodes.values():
            if node not in visited:
                dfs(node)

        return stack[::-1]  # reverse for correct topological order

Kahn’s Algorithm Topological Sort

The general idea is to repeatedly remove nodes from the graph that have all it’s dependencies visited (or no dependencies). We track this by keeping track of the in-degree for each node and then subtracting one each time we visit one of it’s dependencies.

from collections import deque, defaultdict

def kahn_topological_sort(graph):
    in_degree = defaultdict(int)

    # Compute in-degrees of all nodes
    for node in graph.nodes.values():
        for neighbor in node.neighbors:
            in_degree[neighbor] += 1

    # Queue of nodes with in-degree 0
    zero_in_degree_queue = deque([
        node for node in graph.nodes.values() if in_degree[node] == 0
    ])

    topo_order = []

    while zero_in_degree_queue:
        current = zero_in_degree_queue.popleft()
        topo_order.append(current.value)

        for neighbor in current.neighbors:
            in_degree[neighbor] -= 1
            if in_degree[neighbor] == 0:
                zero_in_degree_queue.append(neighbor)

    if len(topo_order) != len(graph.nodes):
        raise ValueError("Graph contains a cycle")

    return topo_order