AVL Trees
The objective of AVL trees is to ensure that the binary search tree is balanced.
This is to ensure that searches for elements within the tree take at most
$O(\lg n)$ running time.
Let's define the height of a sub-tree rooted at position $p$. This is the
number of edges on the longest path from $p$ to a leaf. By this definition,
a left position has height of 0.
Remember that for a balanced binary search every internal position $p$ of
$T$, the height of the children of $p$ differ at most by 1.
AVL trees keep the tree height-balanced to a certain degree. An AVL tree has
balance factor calculated at every node. The balance factor of a node is
calculated as:
$$
\text{height(left sub-tree) } - \text{ height(right sub-tree)}
$$
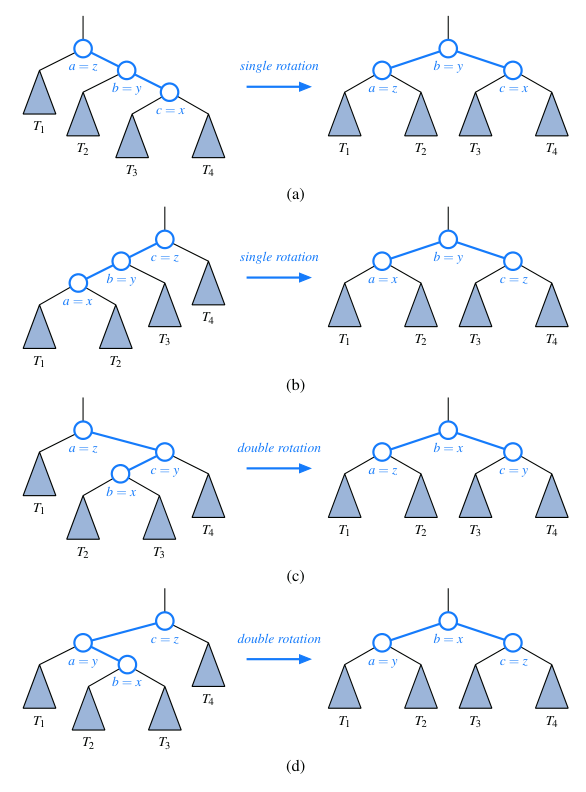
Rotations
To balance a tree when it enters an "unbalanced" state, we use rotations.
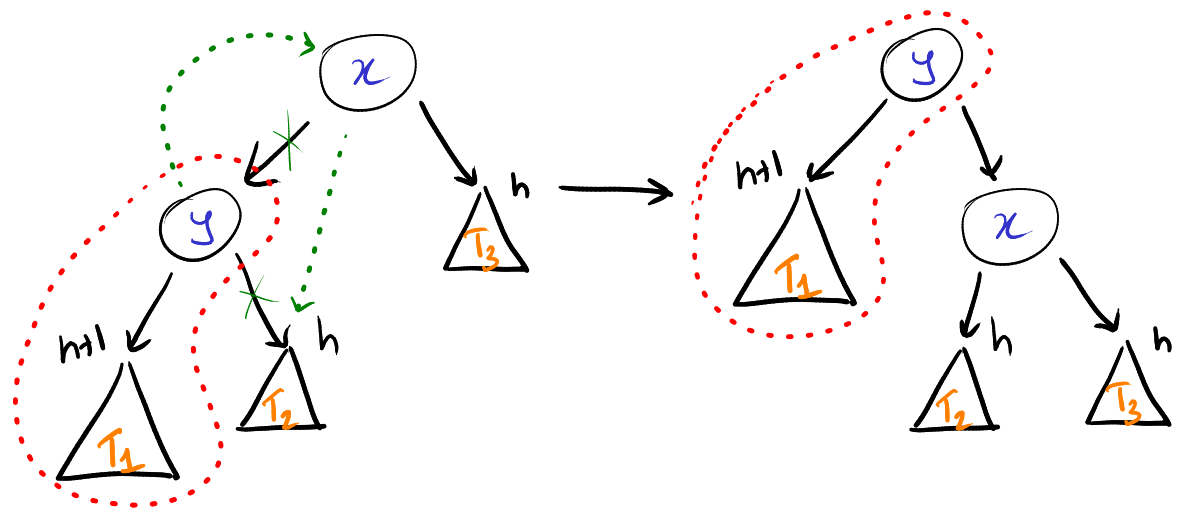
Let the node that needs to be rebalanced be x.
Outside Cases (require single rotation)
- Insertion into left sub-tree of left child of
x.
- Insertion into right sub-tree of right child of
x.
We move the child node of x with the higher height to the root position, we
make the right child of the new root the left child of x.
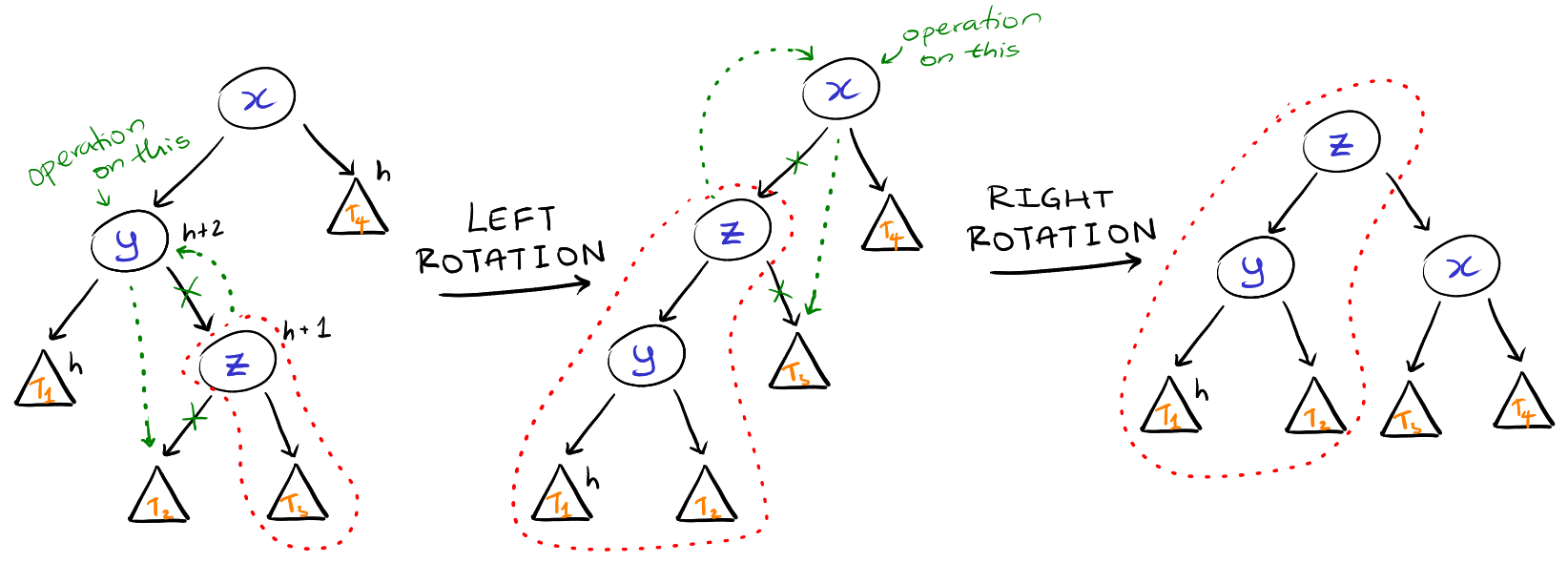
Inside Cases (require double rotation)
- Insertion into right sub-tree of left child of
x.
- Insertion into left sub-tree of right child of
x.
First perform either a left or right rotation to convert it to an outside case
and then perform the other type of rotation. So we'll either perform a left and
then a right rotation or a right and then a left rotation.
Implementation
We need to maintain either the height of the node or the difference in the
heights of the left and right trees. If we choose to maintain the height then we
have to maintain the integer but it makes it easier to read. However, if we
store the difference between the right and left trees, we only need to store a 2
bit number since at any point the values can be -1, 0, 1 since if it ever needs
to go to 2, we need to rebalance.
These values need to be updated each time an insert or delete is performed.