Binary Search Trees

Binary search trees are binary trees that follow a particular rule.

Definition: A binary search tree is a binary tree in which, all the nodes in the left sub-tree of any node is lower than that node and all the nodes in the right sub-tree of any node is higher than that node.

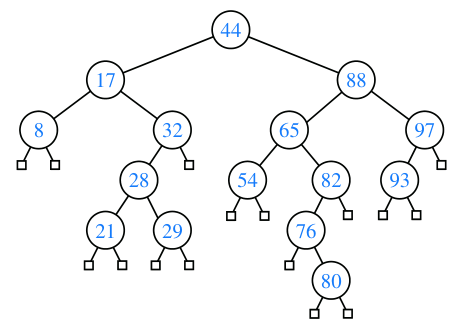
Enforcing this rule allows us to perform searches for an element much faster.

Search Operation

When we search for an element, we can ask the question "is this equal, greater than or less than the search element" and narrow down our search. We can do this because if the key we are looking for is lower than the current node's key then we know that it must be present in the left tree since the right tree only contains keys with greater value. Here is the pseudocode for the algorithm.

// Search for 'key' in binary tree 'T'
search(T, key)
    if T is null
        return null

    if key == T.key
        return T

    else if key < T.key
        return search(T.left, key)

    else
        return search (T.right, key)

This running time for this algorithm is directly dependant on the height of the binary search tree. The greater is the height of the tree the greater is the time to search. At each iteration, we go to the next level in the tree.

Therefore, the worst case running time of this algorithm is $$O(h)$$ where $$h$$ is the height of the binary tree.

Insertion Operation

To insert an element into tree, we just keep following the same principle as the search and if the key is present then we replace the value and if not, then we add it as a left node.

Here is the pseudocode:

// Insert (key, value) pair into binary tree 'T' 
insert(T, key, value)
    if T is null
        // some way to create a tree
        T = Node(key, value)

    if key == T.key
        // Update the value
        T.value = value

    if key < T.key
        if T.left == null
            T.left = Node(key, value)
        else
            insert(T.left, key, value)

    else
        if T.right == null
            T.right = Node(key, value)
        else
            insert(T.right, key, value)

Delete Operation

Deletion is a bit more complicated than search and insert since a node may be deleted anywhere in the tree.

The delete operation differs based on where the node to be deleted is present.

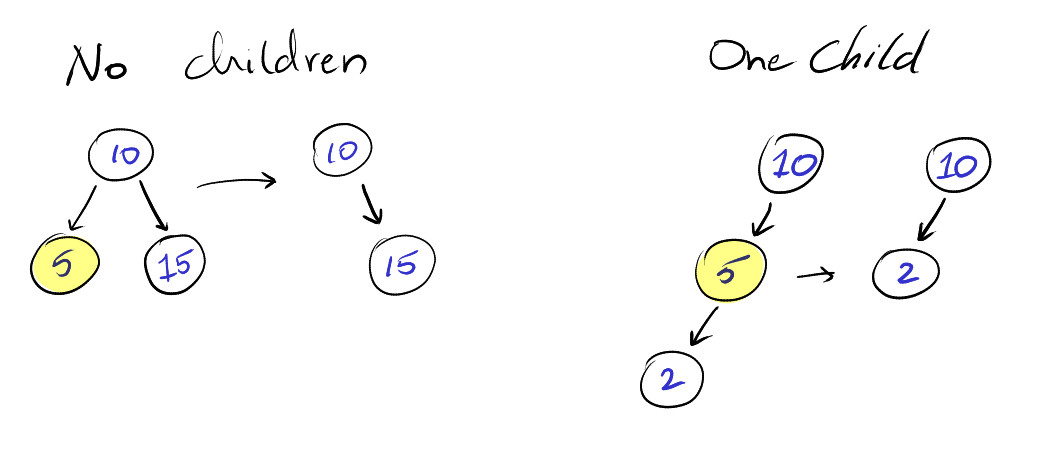
• Leaf Node: If the node to be deleted is a left node, then we can just remove the reference to this node from it's parent.

• Single Child: If the node to be deleted has a single child, then we just have the parent of the node reference the child.

• Two Children: We can either find the max node in the left tree or the min node in the right tree to replace the parent node. Consider the max node in the left tree - since it is the max, the other elements in the left tree are all less than it and since it was in the left tree, all the elements in the right tree are already greater than it.

Here are diagrams representing each of those operations:

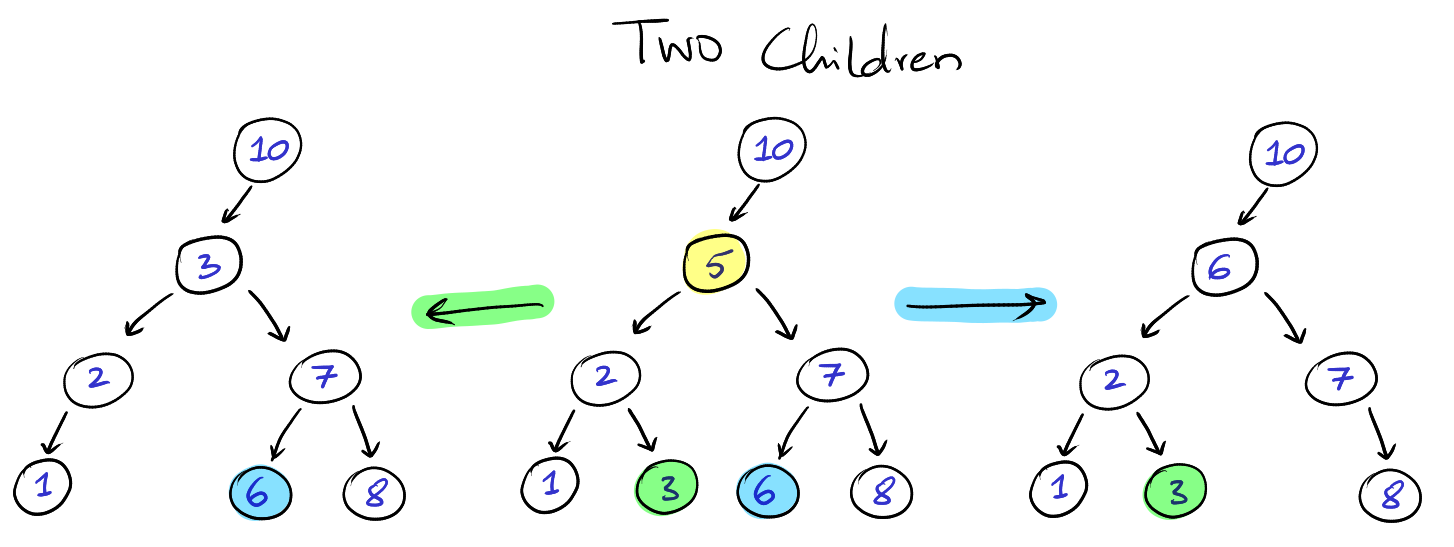
Note that we take EITHER the blue option OR the green option. Either of these elements can be used to replace the deleted node.

Here is the pseudocode for the operation:

// Utility function to find the node with minimum key value
minValueNode(node)
    current = node

    // Loop down to find the leftmost leaf
    while current.left is not null
        current = current.left

    return current

// Delete the node with 'key' from tree 'T'
delete(T, key)
    if T is null
        return

    if key < T.key
        delete(T.left, key)
    else if key > T.key
        delete(T.right, key)
    else
        // Node with only one child or no child
        if T.left is null
            T = T.right
            free(T)
        else if T.right is null
            T = T.left
            free(T)
        else
            // Node with two children: Get the inorder successor (smallest in the right subtree)
            temp = minValueNode(T.right)

            // Copy the inorder successor's content to this node
            T.key = temp.key
            T.value = temp.value

            // Delete the inorder successor
            delete(T.right, temp.key)