Time Complexity

The time complexity of an algorithm is a way of discussing the efficiency of an algorithm. This helps us talk about the way the algorithm scales and how it much longer time it would take on having to process larger data.

O notation

Wikipedia Big O Notation

A function f(n) is said to be of the order g(n) written as, O(g(n)), if there exists positive constants C and n₀ such that f(n) <= C g(n) ∀ n >= n₀.

Big O notation is a mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular value or infinity.

Time Calculations

Calculate the time of a particular algorithm

We can measure the complexity of a particular algorithm by counting the number of basic operations that are performed.

Example Algorithm to find the largest integer in an array of n integers.

public static int findLargest(int[] arr) {
  int largest = arr[0]; int
  index = 1;

      while (index < arr.length) {   // Runs n times
          if (arr[index] > largest)  // Runs n-1 times
          largest = arr[index];      // Runs n-1 times
          index++;                   // Runs n-1 times
      }

      return largest;
}

The sum of the number of operations performed:

n + (n-1) + (n-1) + (n-1) + (n-1) = 4n - 3

We can assume that the time taken to perform all the basic operations takes the same time in most cases. For this particular case, let's assume the time taken for 1 single operation is t.

So, the total time taken by the algorithm would be 4nt - 3t.

When an algorithm performs better for large values of n, it's referred to as the asymptotic complexity.

This would have a Big-O complexity of O(n) since the fastest scaling factor in the terms in the equation is n.

Given Data Size, Estimate Time

If we're given an O notation, the time equation of a given algorithm, and the time for a given input, we can calculate the for a different input size.

Example:

Question: An Algorithm X takes 1 ms for an input size of 1000. Approximate the time taken for an input size of 5000.

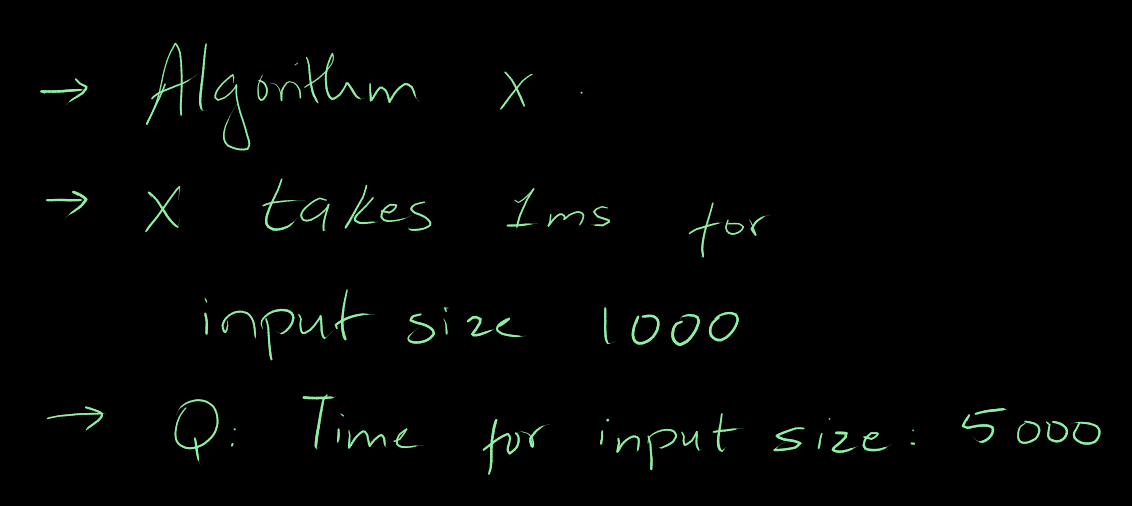
Part 1: If Algorithm X is linear.

Part 2: If Algorithm X is quadratic.

The thing we're doing in the above solution is just finding the time it takes to perform a single step and then multiplying that by the number of total steps. We just do all that in the cross-multiplication.

Data Structures

A data structure is a collection of data items that are grouped together with certain operations defined on them.

Unordered Lists

An unordered list is a simple linear collection of unordered data items.

Operations Defined

• Add an item to the list.
• Remove a specific item from the list.
• Step through all the items.
• Search the list for a specific item.

We can use an Array to represent an unordered list, but since they store successive items in consecutive memory, the deletion of random items requires items to be moved. We can use a linked list to solve this problem.

Linked List

A linked list is a linear data structure consisting of nodes. Each node holds a data item and a link to the next node.

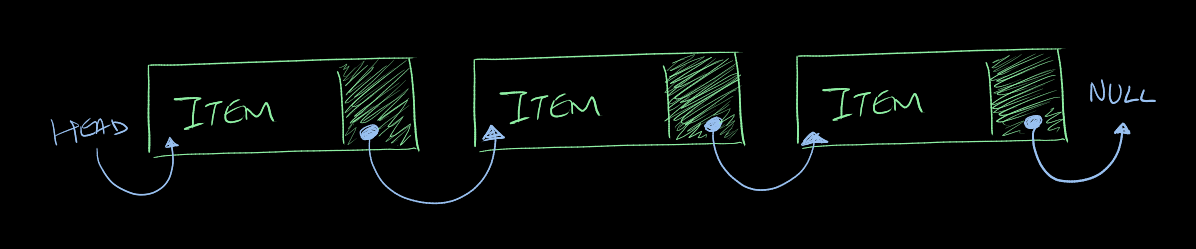
We store a pointer to the start of the linked list, and then each node points to the next. The last node points to null to represent the end of the list.

Advantages

• Memory is allocated and de-allocated on-demand.
• No memory wasted, thanks to the first advantage.
• Items can be inserted and deleted without affecting other entries.

Disadvantages

• Doesn't allow random access of nodes.
• More memory is required compared to an array since you need to store an extra pointer to the next node.

Implementation

Here is an implementation in Java: Suchith Github

There are other languages in which the linked list has been implemented if you look around the same repository.

Ordered Lists

An ordered list is a linear collection of items in which the items are arranged in either ascending or descending order of keys. The key is one part of the item. It servers as the basis of ordering. An ordered list is sorted and maintained sorted, even when new items are added or existing items are deleted. Repetition of keys is usually not allowed.

The primary and pretty much only advantage of ordered lists is that it enables really fast search. This is thanks to an algorithm called "binary search" which takes only O(log(n)) in the worst case. This advantage comes at a cost of inserting and deleting items.

One would use an ordered list in those rare cases where the number of searches are a lot higher than the number of insertions. A great example of this would be google's search engine! The number of searches for a web page is much higher than the number of web pages inserted per day.

For ordered lists to be effective, one would need to use binary search! You can find more information about it here: Binary Search

Advantages

• Fast search for items using binary search.

Disadvantages

• Insertion time is greatly increased.

Implementation

The implementation can be found over here: Suchith Github Ordered List

That particular implementation (at the time of writing 2023-Jun-14) allows duplicate values and uses an ArrayList in java to hold the values of the elements. It uses binary search whenever possible.

Merging Ordered Lists

We can use an algorithm called the "Two-finger-walking algorithm" to merge two ordered lists. It just keeps comparing the front elements of the lists and adding it to a new list.

You can find the implementation in the same file as the Ordered list implementation.

Trees

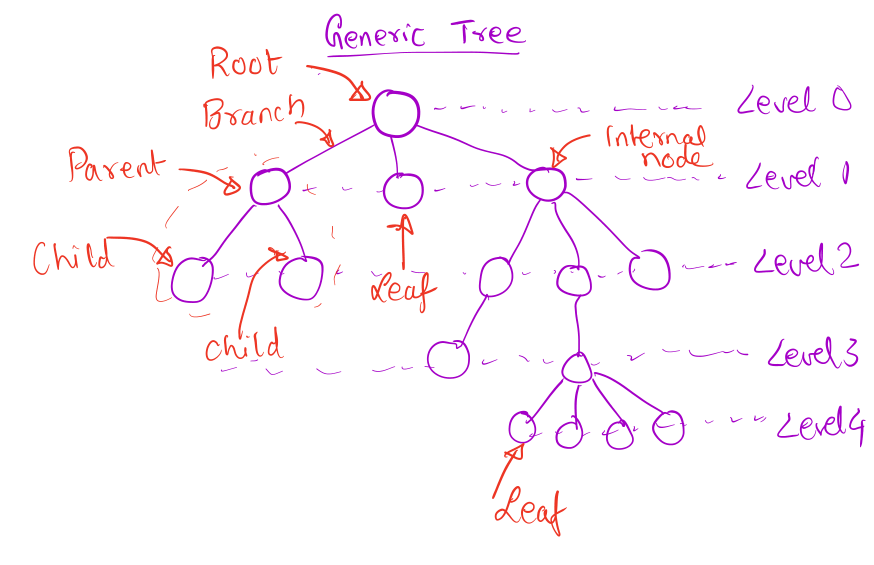
A tree is a data structure consisting of a set of nodes arranged in a hierarchy. There is one special node called the root which is the starting point of the tree and the root is connected to zero or more nodes at the next level by branches or links. Similarly, each node at Level i is connected to zero or more nodes at Level i+1.

• A parent node is the node that the current node is connected to at a level lower to its level.
• A child node is a node that the current node is connected to at a level higher to its level.
• A leaf node is a node that does not have any children.
• Non-leaf nodes are called internal nodes.

Binary Trees

A binary tree is a tree in which every node has at most two children. The maximum number of nodes in a binary tree of height h is 2^(h+1) - 1

Special Types of Binary Trees

• Strictly Binary Tree: A tree in which every node has either no children or exactly two children.

• Complete Binary Tree: In a complete binary tree, every level but the last must have the maximum number of nodes possible at that level. The last level may have fewer than maximum possible, but they should be arranged from left to right without any empty spots.

Binary Search Tree

A binary search tree (BST) is a binary tree that is sorted or ordered according to a rule. In general, the information contained in each node is a record - one part is called the key.

A BST is a binary tree in which, for every node x:

• The keys in all the nodes in the left subtree of x are smaller than the key in x.
• The keys in all the nodes in the right subtree of x are larger than the key in x.

Example of a binary search tree:

Binary Search Tree

Source: Wikipedia

The binary search tree basically facilitates easier searching of elements, similar to the binary search algorithm.

Search

• Compare the target key with the value in the root.
• If it is equal, target found.
• If an empty subtree is reached, target not found.
• Otherwise,
• if target is lesser than value, search left subtree.
• if target is greater than value, search right subtree.

Insertion

We just perform the search algorithm as metioned above and then insert it at the location where the search "ends" (fails).

Note that a new node always becomes a lead node in the BST.

Deletion

Case 1: X is a leaf node

Simply delete X, that is, detach X from its parent.

Algorithms

A binary tree traversal is a systematic method of visiting and processing each node in the tree.

• Pre-order Traversal

Order: Root-Left-Right.

Visit the root, traverse the left subtree, traverse the right subtree.

• In-order Traversal

Order: Left-Root-Right.

Traverse the left subtree, Visit the root, traverse the right subtree.

• Post-order Traversal

Order: Left-Right-Root.

Traverse the left subtree, traverse the right subtree, Visit the root.

Implementation

Github Suchith Binary Tree This implementation uses a recursively defined class BinaryTree.

Huffman Encoding

This is a method of encoding/compressing ASCII data using binary trees. Here's the article on it: Huffman Encoding Suchicodes

Algorithms

Searching Algorithms

Binary Search

Binary Search is an algorithm that requires an ordered list of elements. This algorithm takes advantage of the fact that in an ordered list all elements before any elements x are smaller than x and any elements after x are greater than x.

In each iteration, we look at the middle element and decided whether to discard the top half since the element we're looking for is smaller or discard the bottom half since the element is larger.

Binary search as a big O complexity of O(log n)!

Idea

Problem: We're trying for find an element x in a sorted list.

1. Look at the middle of the list.
2. If x is the element in the middle then found.
3. If x is lower/less than the middle element, discard everything after the middle element.
4. If x is higher/greater than the middle element, discard everything before the middle element.
5. Go to step one if more elements present. If not, element not found.

Implementation

The implementation can be found over here: Suchith Github Binary Search

This particular implementation assumes that the list provided is sorted.