Three Sum
- Problem Number: 15
- Difficulty: Medium
- URL: 3sum
A friend of mine, Brahmpreet, and I were working on this problem together. This
is a summary of our approaches and solution.
Problem statement
Given an integer array nums, return all the triplets [nums[i], nums[j], nums[k]]
such that i != j, i != k, and j != k, and nums[i] + nums[j] + nums[k] == 0.
Notice that the solution set must not contain duplicate triplets.
Example 1:
Input: nums = [-1,0,1,2,-1,-4]
Output: [[-1,-1,2],[-1,0,1]]
Explanation:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0.
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0.
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0.
The distinct triplets are [-1,0,1] and [-1,-1,2].
Notice that the order of the output and the order of the triplets does not matter.
Example 2:
Input: nums = [0,1,1]
Output: []
Explanation: The only possible triplet does not sum up to 0.
Example 3:
Input: nums = [0,0,0]
Output: [[0,0,0]]
Explanation: The only possible triplet sums up to 0.
Constraints:
3 <= nums.length <= 3000-10^5 <= nums[i] <= 10^5
Initial Approach
Our initial approach was the most straightforward approach. Fix a certain
element (say first) and then look a pair of numbers that sum to -first
(since the total sum has to be 0). Then, fix a second element (say second) and
look for the third number to be -first - second.
Pseudocode wise, the solution looks like this:
function threeSum(nums[0..n])
triples = []
for i <- 0 to n
for j <- i to n
for k <- j to n
if (nums[i] + nums[j] + nums[k] == 0):
push(triples, [nums[i], nums[j], nums[k]])
return triples
Now, this doesn't account for the problem with duplicates just yet. But here is
that solution coded in Go:
func threeSum(nums []int) [][]int {
list := [][]int{}
for i := 0; i < len(nums); i++ {
doubleList := twoSum(nums, -nums[i], i+1)
for _, double := range doubleList {
newTriple := []int{nums[i], double[0], double[1]}
list = append(list, newTriple)
}
}
return list
}
func twoSum(nums []int, target int, start int) [][]int {
list := [][]int{}
for j := start; j < len(nums); j++ {
if (oneSum(nums, target - nums[j], j+1)) {
list = append(list, []int{nums[j], target - nums[j]})
}
}
return list
}
func oneSum(nums []int, target int, start int) bool {
for k := start; k < len(nums); k++ {
if (nums[k] == target) {
return true
}
}
return false
}
To fix the problem with the duplicates, we just added a check before adding it
to our final answers lists. We compared the elements of the triples and checked
if they were duplicates for each existing triple.
func compareTriples(first []int, second []int) bool {
match := -1
for i, num := range second {
if first[0] == num {
match = i
break
}
}
if (match == -1) {
return false
}
for j, num := range second {
if first[1] == num && match != j {
return true
}
}
return false
}
func findTriple(listOfTriples [][]int, newTriple []int) bool {
for _, triple := range listOfTriples {
if compareTriples(triple, newTriple) {
return true
}
}
return false
}
You can see that we only need to check the first two elements since the sum of
all triples are 0, we can be sure that the third element has to be the same.
Now, we just add this check before we append a triple to our answers list.
newTriple := []int{nums[i], double[0], double[1]}
if (!findTriple(list, newTriple)) {
list = append(list, newTriple)
}
Analysis
We see that we have three loops and then another look to check if the triple is
already present. Therefore the overall running time of this algorithm is going
to be $O(n^3) + O(n \cdot k)$ where $k$ is the number of triples present. This
assuming that the compareTriples function runs in $O(1)$ and the findTriples
runs in $O(n)$. This is a reasonable assumption since compareTriples has to
always only compare three elements.
This solution failed on leetcode due to "time limit exceed" problem.
We had to find a way to make this faster.
Second Approach
The first thing we tried to speed up was actually the $O(n \cdot k)$ part since
we weren't sure where to start with the $O(n^3)$. We wanted use some form of
hash set so that we can check if a triple is already present without having to
check the entire list.
Two triples are the same if the contain the same numbers, the order of the
elements do not matters, just their presence. So (7, -3, -4) and (-3, 7, 4)
should be considered the same triple.
Our initial thought was to use a bit-vector but the universe size was $2 \cdot
10^5$. This would be too large to maintain a bit vector for.
We were trying to find mathematical properties of the triples that would help us
encode it. Things like sum, product, xor, but nothing seemed to create a unique
result.
Finally, we observed that the range was within $10^6$, which $\log_2(10^6)
\approx 19.9$ and $\lceil \log_2(10^6) \rceil = 20$ and we have three numbers,
therefore, $20 * 3 = 60$ bits would be required to store all three numbers.
This meant that we could store all the three numbers side-by-side in a single
int64 variable.
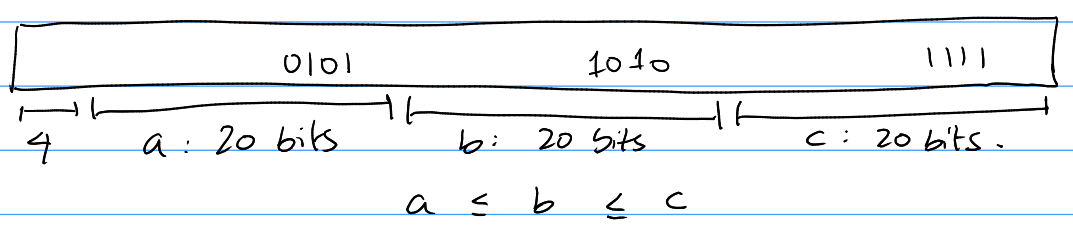
Now, we coded this in Go:
type hashSet map[int]struct{}
func (set hashSet) add(item int) {
set[item] = struct{}{}
}
func (set hashSet) remove(item int) {
delete(set, item)
}
func (set hashSet) contains(item int) bool {
_, found := set[item]
return found
}
func hashTriple(triple []int) int {
sort.Ints(triple)
var value int = 0
value += triple[0]
value += triple[1] << 20
value += triple[2] << 40
return value
}
Now instead of performing a linear search for the triples we've already
calculated we can just check the hash set for its existence. Notice that we use
bit shifts to move the numbers over so that each of them can slot into their
sections. An int in Go is 64 bits by default, however, it is recommended that
you be explicit when doing things like bit level manipulation. Therefore, using
int64 instead of int would have been a better idea, but that required us to
cast the numbers.
Analysis
Using the hash set got rid of the linear check and reduced the $O(n \cdot k)$ to
a $O(n \cdot 1)$. However, this unfortunately didn't solve our problem as we
suspected. The main offender for the time complexity was the cubic search for
the triples.
This failed on leetcode for the same time constraint issue.
Final Approach
After trying a lot of different ideas such as adding all the elements into a
hash set initially with a linear scan - to make the last level search faster to
adding the pairwise sums to a hash set, etc. None of those ideas would work.
Finally, we realized that the solution was right under our noses the whole time.
We have solved the problem of twoSum before. That usually only requires you to
check if a target sum is present in the list. It's not designed to find all
unique combinations the would sum to that value. Our twoSum function from
above is required to find all the unique combinations that add up to a target.
One of the solutions for the two sum problem to be completed in linear time is
to first sort the list and then have a low and high pointer initialized at the
start and end of the list respectively. Then we find the sum of the current
positions (say sum). If sum < taget then we need to move the left pointer
right. If sum > target then we need to right pointer left. If sum == target,
then we have found the sum.
We modify this solution to move both left and right points when sum == target
since this will allow us to continue and find other solutions that result in
this target sum. We stop searching when left > right.
func twoSum(nums []int, target int, start int) [][]int {
list := [][]int{}
left, right := start, len(nums) - 1
for left < right {
sum := nums[left] + nums[right]
if (sum < target) {
left++
} else if (sum > target) {
right--
} else {
list = append(list, []int{nums[left], nums[right]})
left++
right--
}
}
return list
}
We just modified this twoSum function to be a linear function rather than a
quadratic function.
Analysis
The outer threeSum function contains a loop that runs $n$ times. The inner
twoSum function in-turn runs $n-i$ times, where $i$ is the starting index.
Therefore, this speeds up our initial $O(n^3)$ running time to a $O(n^2)$. This
twoSum function requires the list to be sorted, therefore, we sort the list
at the start of the threeSum function.
This combined with our hashing function now has a overall running time of:
$$
O(n \lg n) + O(n^2) + O(n \cdot 1) = O(n^2)
$$
This finally passed on leetcode without failing to meet the time restriction.
Further Improvements
After looking at some of the best solutions, we found that there were some minor
additions and deletions that would lead to a lot better time.
-
Remove the sort in the hashTriple function: We can do this due to the way
we are constructing the triple and the fact that the entire list is sorted.
-
Skip duplicate elements inside the twoSum function to avoid matching
duplicates. That is, once we find the target element we move the left and
right pointers until a different element is being pointed to by both these
pointers. This can be done since the overall list is sorted.
-
Skip duplicate elements inside the threeSum initial loop. This is similar
to the previous point and we can just skip elements that we're already
started with.
-
Remove the hash set entirely. Once we skip the duplicate elements at both
positions there is no reason to check the hash table since there is no way
for a duplicate triple to exist.
Here are the changes, indicates with comments Addition 1 and Addition 2:
import "sort"
func threeSum(nums []int) [][]int {
list := [][]int{}
sort.Ints(nums)
for i := 0; i < len(nums); i++ {
// Addition 1
if (i > 0 && nums[i] == nums[i-1]) {
continue
}
doubles := twoSum(nums, -nums[i], i+1)
for _, double := range doubles {
newTriple := []int{nums[i], double[0], double[1]}
list = append(list, newTriple)
}
}
return list
}
func twoSum(nums []int, target int, start int) [][]int {
list := [][]int{}
left, right := start, len(nums) - 1
for left < right {
sum := nums[left] + nums[right]
if (sum < target) {
left++
} else if (sum > target) {
right--
} else {
list = append(list, []int{nums[left], nums[right]})
// Addition 2
for left < right && nums[left] == nums[left+1] {
left++
}
for left < right && nums[right] == nums[right-1] {
right--
}
left++
right--
}
}
return list
}
Analysis
According to my analysis this doesn't actually speed up the asymptotic running
time of the algorithm since it's still $O(n^2)$. However, changing from a
hash set and memory allocation to just an increment to skip duplicates is going
to increase performance by quite a lot!
On leetcode our running time went from 449ms to 45ms which is an order of
magnitude lower. However I think if we scale the number of elements, the
difference is going to be a constant factor and not more than that.
There are more improvements that can be done to this solution:
We allocate and deallocate (garbage collect) new lists for every time we find a
double. This can be moved into the threeSum function to reduce memory
consumption and reduce the overhead of allocation and deallocation.
That said, we're going to call it a day!
Solution
This was the our final solution which was able to complete the task in 49ms
using 7.6 MB RAM on leetcode.
Note that this can be made more efficient by moving the twoSum code into the
threeSum function to reduce function calls and memory allocations.
import "sort"
func threeSum(nums []int) [][]int {
list := [][]int{}
sort.Ints(nums)
for i := 0; i < len(nums); i++ {
if (i > 0 && nums[i] == nums[i-1]) {
continue
}
doubles := twoSum(nums, -nums[i], i+1)
for _, double := range doubles {
newTriple := []int{nums[i], double[0], double[1]}
list = append(list, newTriple)
}
}
return list
}
func twoSum(nums []int, target int, start int) [][]int {
list := [][]int{}
left, right := start, len(nums) - 1
for left < right {
sum := nums[left] + nums[right]
if (sum < target) {
left++
} else if (sum > target) {
right--
} else {
list = append(list, []int{nums[left], nums[right]})
for left < right && nums[left] == nums[left+1] {
left++
}
for left < right && nums[right] == nums[right-1] {
right--
}
left++
right--
}
}
return list
}