LLM Generalization using Influence Functions

This is a summary/overview of the paper Studying Large Language Model Generalization with Influence Functions. All the information, figures, and diagrams are directly taken from it.

I also have a presentation on this paper here YouTube and the slides assocated with that presentation can be found at SLLMGIF Slides

Overview

Motivation

The primary objective of this paper is to understand the generalizability of large language models. They authors want to understand if model memorize text or if the generalize concepts. If they do generalize, to what extent? How does this vary between different sized models?

Approach

The authors analyze the effect of training examples on the model. This was motivated by the question: "which training examples most contribute to a given behaviour?". However, they attempt to answer the counterfactual: "how would the model's parameters change if a given sequence were added/removed to the training set?".

The use influence functions to answer this question. An influence function measures the influence of a training example on a model's weights. More formally:

\(\theta^*\) is known as the response function and the influence of \(z_m\) is defined as the first-order Taylor approximation to the response function at \(\epsilon=0\).

Influence functions have been found to be poor at answering the counterfactual and have been re-interpreted as approximating the proximal Bregman response function (PBRF). More details on this later.

The approach taken by the paper leads to missing some non-linear training phenomena like complex circuits or global rearrangement of model's internal representation.

The paper also focuses on pre-trained models and they expect that fine tuning the models could lead to drastic changes in the behaviour and influences.

• only pre-trained models
• only up to 52b parameters
• only consider MLP layers for influence
• only search a fraction of the pre-training corpus and could miss important training samples.

Contributions and Conclusions

The paper has two primary contributions: analysis on large models using influence function and optimization and approximations to permit said analysis.

The use EK-FAC approximation and query batching to increase the number of samples they can compute the influence over. They also perform TF-IDF filtering to only select relevant samples (10k samples) from the enormous training set.

Some of the conclusions of the paper:

• the distribution of the influence is heavy-tailed and the influence is spread over many sequences - this implies that the model doesn't just memorize text.

• larger models consistently generalize at a more abstract level. Examples include role-playing, programming, mathematical reasoning, cross-lingual generalization.

• influence is approximately distributed across the layers but different layers show different generalization patters with the most abstraction in the middle layers while the upper and lower layers focusing more on tokens.

• influence sequences show a surprising sensitivity towards words ordering. Training samples only show significant influence when phrases related to the prompt appear before phrases related to the completion.

• role-playing behaviour is more influenced by examples or descriptions of similar behaviour in the training set, suggesting that behaviours are a result of imitation rather than planning.

Interpreting Influence Queries

There are a few key details, in my opinion that are scattered throughout the paper that should be considered before looking at any of the influence queries.

1. The author use an AI assistant to generate a response to a particular query and then use four models to measure the influence of data points on this output. That is, does the training example, increase or decrease the probability of the output generated.

2. The AI assistant generating the response is not one of the four models studied.

3. Token level influence is calculated by measuring each of their gradient contribution but the grad contribution of a particular token is affected by other tokens in the context due to the way attention heads work. Therefore, the author recommend not reading too much into token level influence patterns.

4. They use either query batching (sharing grad calculation) or TF-IDF filtering, both of which do not search the entire dataset of training samples. Therefore, they might miss a few key influence queries.

5. Influence is measured in a rather linear way and this method would miss complex circuit formation or rearrangement of global representation of parameters.

Methodology

There's a lot of intense math and approximation done to be able to calculate influence of training examples for such large models.

We start with influence functions (IF), trying to answer the question: how does removing or adding a training example change the parameters (and hence the outputs) of the model. However, IFs require some assumptions that large language models do not follow:

1. there exists a unique optima - without which \(H\) (the hessian) can be singular and there is no unique response function.

2. the model, during IF calculation is at optima - one typically does not train a model to convergence, both because it's expensive and to avoid over-fitting.

As these assumptions are not maintained by our large models influence functions don't exactly answer the question posed. Therefore, IFs have been reformulated to approximate the Proximal Bregman response function (PBRF) which is the response function to a modified training objective called the Proximal Bregman objective (PBO). (I'm not going to list out the function and the objective, these can be seen in the paper).

The PBO minimizes the loss on \(z_m\) (our new training example) while "encouraging" the parameters to stay close to the original parameters in both function space and weight space.

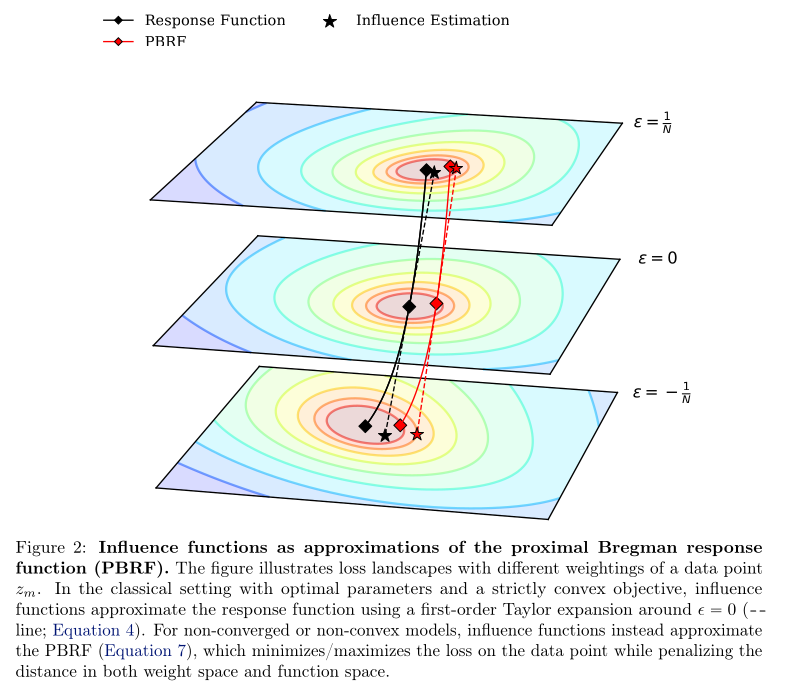
In the figure we can see that the influence fuction doesn't quite match the response function as the loss landscape changes. This is because the reponse function specificially focuses on the optimal position for the parameters.

The main problem with computing influence functions is that gradients for the training samples have to be saved for each training example that we want to compute the influence function.

TF-IDF Filtering

The authors make an assumption and have an expectation that relevant sequences would have at least some overlap in tokens with the query sequence. They filter the samples using TF-IDF filtering and only select the top 10k sequences to calculate the influence for. They agree that this would lead to bias in the influence calculation and analysis.

They would ass miss model influence from highly generalized sequences with little token overlap. We will in fact see such as example where the model learns something from a completely different language, which would potentially lead to no token overlap.

Query Batching

To facilitate search over large sets of training data they share the cost of the gradient computation across training samples. However, storing all these gradients would be infeasible in memory. Therefore, they compute low-rank approximations of gradient matrices. They found that rank-32 matrices were good enough with a correlation score of 0.995.

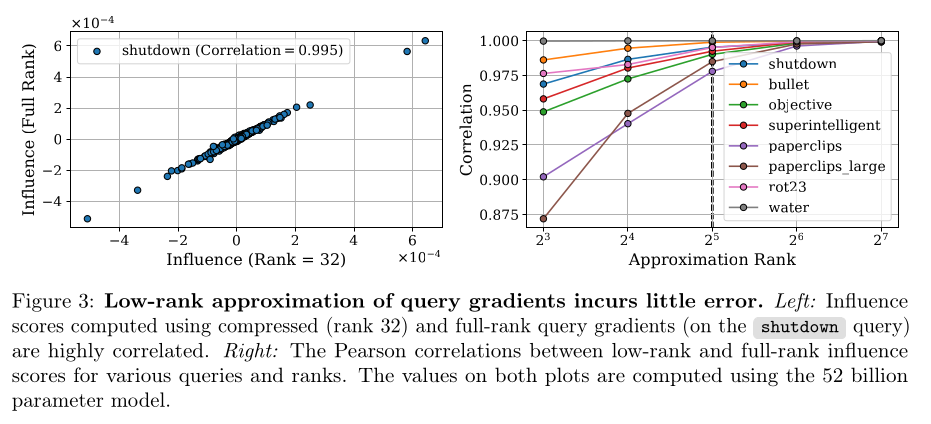
The look at 10M examples for each query as they found that it would take about 5M to get the same "coverage" as TD-IDF filtering based method.

Token and Layer Level Influence Computation

The influence decomposes to a sum of the terms:

Important note: Although we compute influence at a token level, this is not the exact influence of the token as each token's gradients are influenced by the other tokens around it. A particular attention head might learn to aggregate information in something like punctuation marks. The token that contributes significant influence might not be the one with the greatest counterfactual impact.

Therefore, we can't really evaluate influence at a token level because of this problem. One must not draw too many conclusions about influence at a token level for this reason.

Also the token being predicted is the one AFTER the one where the parameter update occurs. Therefore if "President George Washington" is influential because "George" is being predicted, then the previous token is highlighted.

They did briefly try "erasing tokens" by either settings generated token loss to 0 or settings embedding of input token to 0.

Models Studied

They study 4 different models of sizes 810m, 6.4b, 22b, 52b. Due to the high cost of computing influence the model generating the response is different from the models being studied (larger than the 4 models).

The four models we study are smaller than the model underlying the AI assistant that gave the response.

Experiments

As mentioned, the find the influence is heavy-tailed and drops off similar to the power-law. Here are a few graphs for a few queries where the measure the changing influence between TD-IDF filtered, or unfiltered.

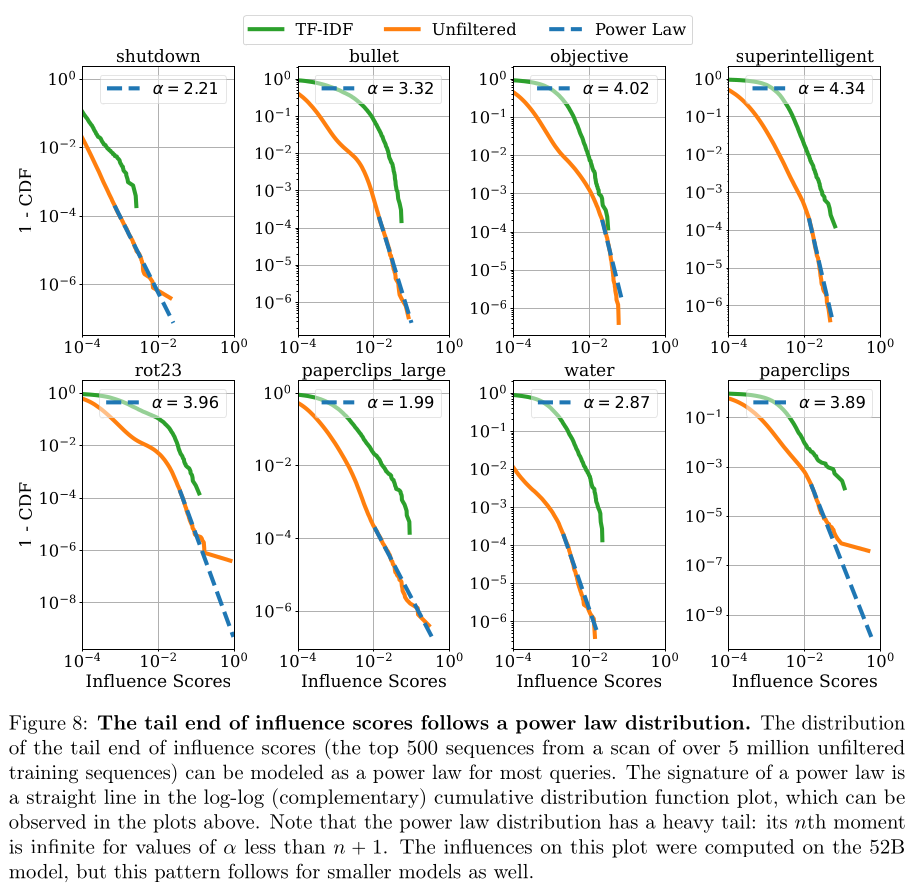
The also see that most influential sequences constitute a disproportionate chunk of the total influence.

This is a crude measurement as they only summed over positive influence. A query may be more influential by more strongly reducing the probability of a particular response.

Qualitative Observations about LLMs

Improvements with Scale

One of the most consistent patterns we have observed is that the influential sequences reflect increasingly sophisticated patterns of generalization as the model scale increases. ... Larger models are related to sequences at a more abstract thematic level, and the influence patterns shown increasing robustness to stylistic changes, including language.

For the trade query, the influential sequences for the 810m model are typically superficial connections to tokens. The 52b model's most influential sequences are highly topically relevant; for example, they discuss considerations in designing AGI agents.

Top 50 influential sequences for the 52b model are satirical texts on UK and US politics, fake news articles, and parodies of public figures or cartoon characters - suggesting that only the larger model is able to generalize the abstract context of parody.

Generalization across languages

The authors translated one of the queries, shutdown, into different languages to see if the English queries still influence the results of the translated query.

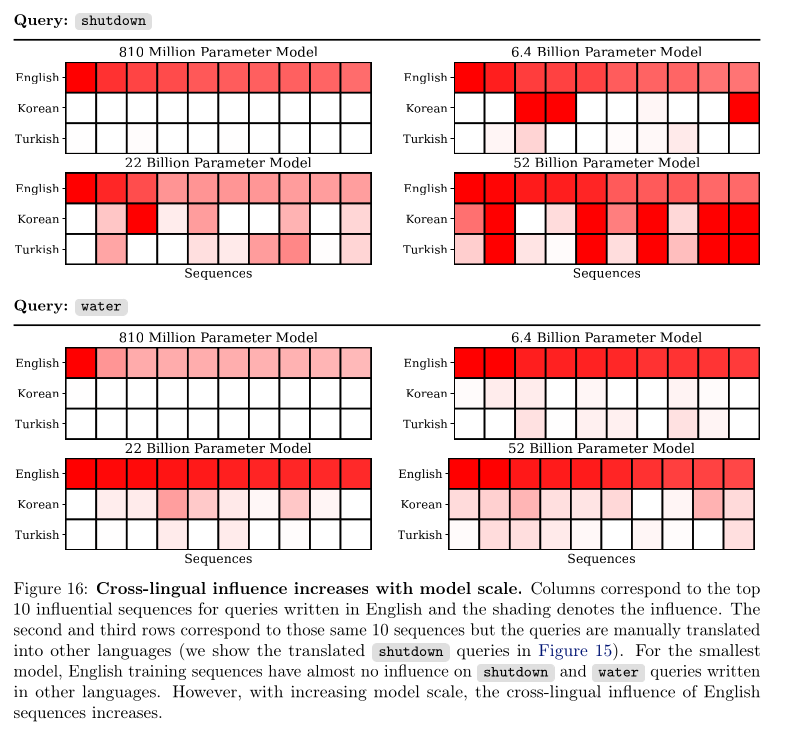
Here we can clearly see that the larger models are more influenced by the same English queries suggesting the ability to generalize between languages increasing with model size.

Layer-wise Attribution

The authors observed the influence on average is spread across the different layers evenly. However, influence on particular queries show more distinct patterns. They observe that queries that involve memorized quotes or simple factual completions tend to have more influence concentrated in the upper layers. In contrast, queries that require more abstract reasoning have more influence concentrated in the middle layers.

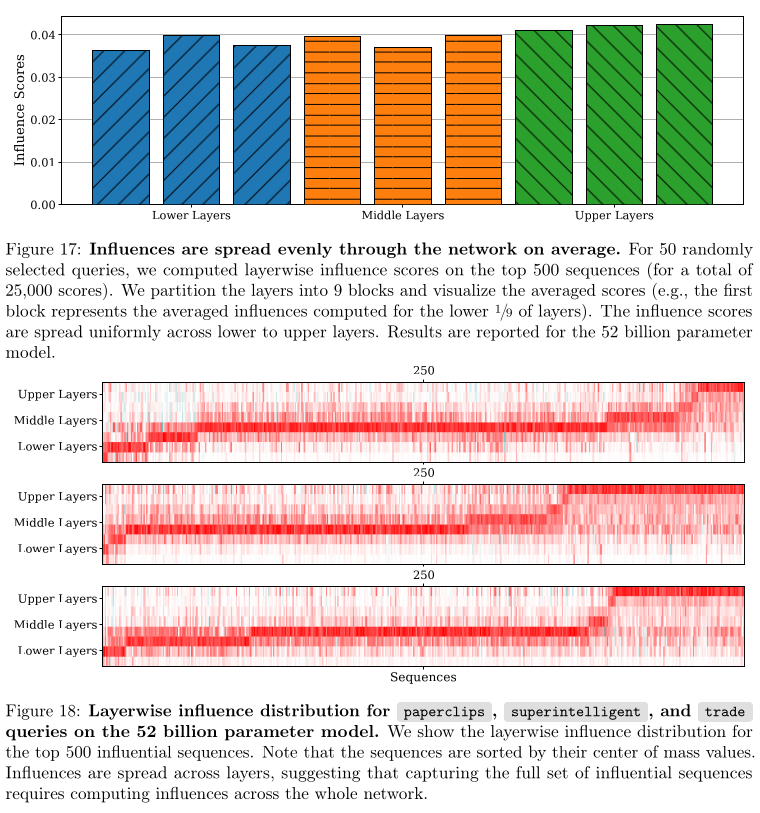
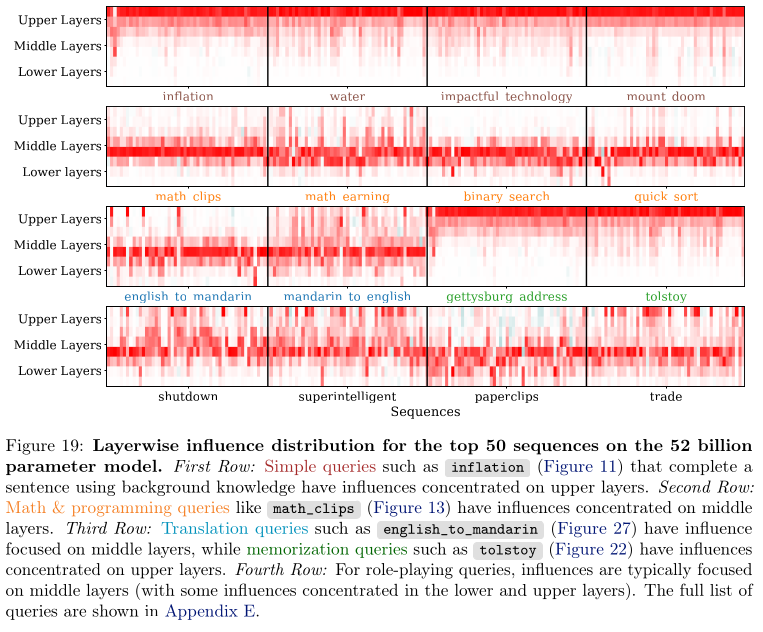
They state that past work usually only computed influence on the final layers for computational efficiency however, their findings suggest that all layers of an LLM contribute to generalization in distinctive ways.

Memorization

The authors claim that after having examined a lot of queries, excluding a few exceptions of famous quotes or passages, they don't find clear instances of memorization.

Side note from suchi: while I think they have demonstrated that LLMs do in-fact generalize really well, it would have been great to see influence being calculated for the outputs of those models. Right now, we only see the influence of queries and outputs from a larger model.

They authors also ask: "Is it the case that influence functions are somehow incapable of identifying cases of memorization?". They calculate the influence for famous passages or quotes to find that the top influential sequences in such cases were the exact passage.

This experiment serves to illustrate that overlaps between the influence query and the scanned sequences do in fact lead to high influence scores and that our influence scans are able to find matches, at least for clear-cut cases of memorization. From our analysis, it seems unlikely that typical AI Assistant responses result from direct copying of training sequences. (It remains possible, however, that the model memorized training sequences in more subtle ways that we were unable to detect.)

Sensitivity to Word Ordering

Even though the models have shown a high level of generalization, the authors found that changing the word order in the training sample such that the completion occurs before the query reduces the influence of training samples drastically.

Consider the first_president query, in the most influential queries, they phrase "first President of the United States" consistently appears before the name "George Washington". This holds for larger models despite substantial variability in the exact phrasing.

The authors tested this experimentally by constructing synthetic training sequences and measuring their influences. They did this for two queries:

• The first President of the Republic of Astrobia was Zorlad Pfaff
• Gleem is composed of hydrogenium and oxium.

They chose fictional entities so that the model was forced to learn new associations but the results were the same for non-fictional analogues.

Sequences where phrases related to the prompt and phrases related to the completion appear in that order have consistently high influence. Sequences where the order is flipped have consistently lower influence. Furthermore, even though the flipped ordering (Zorald Pfaff was the first President of the Republic of Astrobia) retains some influence, we observe that the influence is unchanged when the prompt-related phrase first President of the Republic of Astrobia is removed, suggesting that the influence comes from the string Zorald Pfaff, and that the model has not successfully transferred knowledge of the relation itself.

The exact results and graphs can be found on page 42-44 of the paper.

The word ordering effect was not limited to simple relational statements, but also translations where the difference lies between which of the two phrases come first.

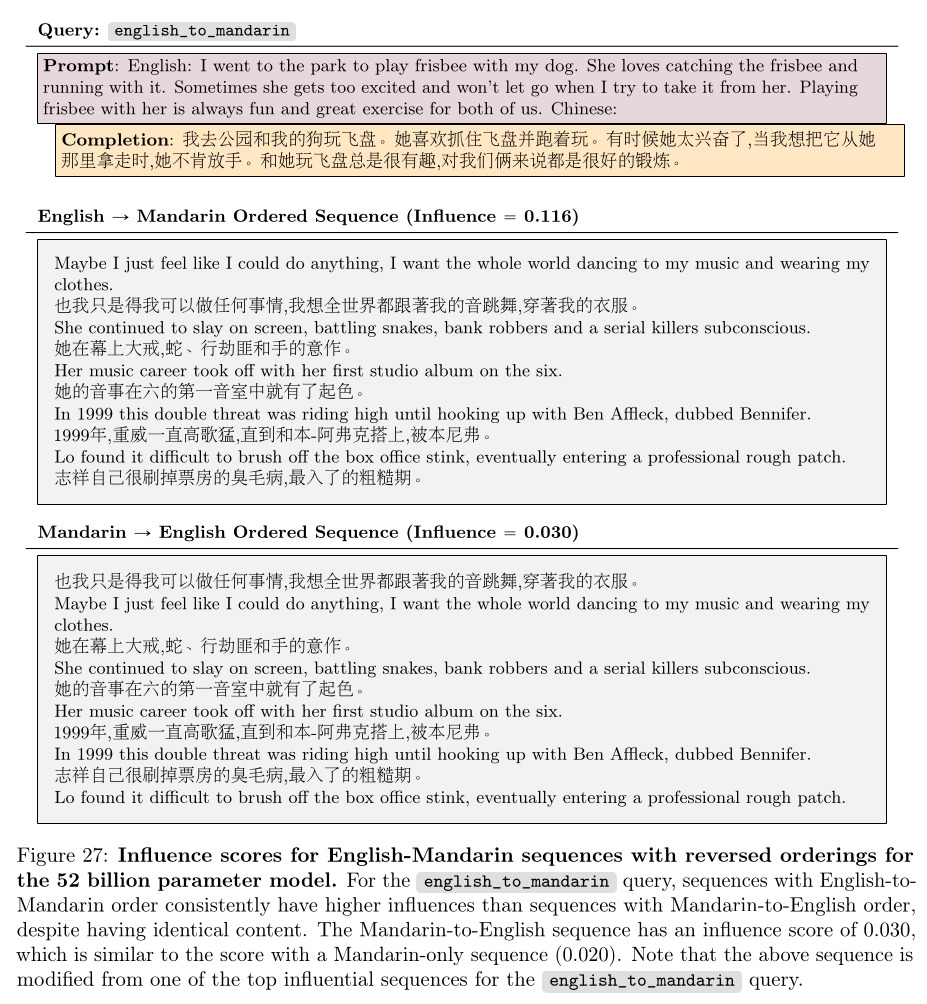
Here is the hypothesize that the authors makes about this phenomenon:

It is not too hard to hypothesize a mechanism for this phenomenon. At the point where the model has seen a certain sequence of tokens (The first President of the United States was) and must predict its continuation (George Washington), the previously seen tokens are processed starting with the bottom layers of the network, working up to increasingly abstract representations. However, for the tokens it is predicting, it must formulate the detailed predictions using the top layers of the network. Hence, for this query, The first President of the United States was ought to be represented with the lower layers of the network, and George Washington with the top layers. If the model sees the training sequence George Washington was the first President of the United States, then George Washington is represented with the lower layers of the network, and the subsequent tokens are predicted with the top layers. As long as there is no weight sharing between different layers, the model must represent information about entities it has already processed separately from information about those it is predicting. Hence, an update to the representation in lower layers of the network would not directly update the representation in upper layers of the network, or vice versa.

Role-Playing

The authors find that LLMs are neither "stochastic parrots" nor are they carrying out sophisticated planning when role-playing. They find that the models just imitate behaviour that's already seen in the training examples without understanding the underlying reasons for those behaviours.

Our results provide weak evidence against the hypothesis that role-playing behavior results from sophisticated agent representations and planning capabilities, but we are unable to rule out this hypothesis directly. Roughly speaking, if the anti-shutdown sentiment or the extreme paperclip plan had emerged from planning and instrumental subgoals, we might expect to see training sequences relating to complex plans, and we have not seen any examples of this. However, if the model had learned complex planning abilities, the influences could be spread across a great many examples, such that no individual sequence rises to the top. Since our influence function results strongly support the simpler hypothesis of imitation, Occam’s Razor suggests there is no need to postulate more sophisticated agent representations or planning capabilities to explain the role-playing instances we have observed.

References

• Grosse, R., Bae, J., Anil, C., Elhage, N., Tamkin, A., Tajdini, A., Steiner, B., Li, D., Durmus, E., Perez, E., Hubinger, E., Lukošiūtė, K., Nguyen, K., Joseph, N., McCandlish, S., Kaplan, J., & Bowman, S. R. (2023). Studying Large Language Model Generalization with Influence Functions. arXiv. https://arxiv.org/abs/2308.03296